46. Job Search V: Modeling Career Choice#
In addition to what’s in Anaconda, this lecture will need the following libraries:
!pip install quantecon jax
46.1. Overview#
Next, we study a computational problem concerning career and job choices.
The model is originally due to Derek Neal [Neal, 1999].
This exposition draws on the presentation in [Ljungqvist and Sargent, 2018], section 6.5.
We begin with some imports:
import matplotlib.pyplot as plt
import jax.numpy as jnp
import jax
import jax.random as jr
from typing import NamedTuple
from quantecon.distributions import BetaBinomial
from scipy.special import binom, beta
from mpl_toolkits.mplot3d.axes3d import Axes3D
from matplotlib import cm
# Set JAX to use CPU
jax.config.update('jax_platform_name', 'cpu')
46.1.1. Model features#
Career and job within career both chosen to maximize expected discounted wage flow.
Infinite horizon dynamic programming with two state variables.
46.2. Model#
In what follows we distinguish between a career and a job, where
a career is understood to be a general field encompassing many possible jobs, and
a job is understood to be a position with a particular firm
For workers, wages can be decomposed into the contributions of job and career
\(w_t = \theta_t + \epsilon_t\), where
\(\theta_t\) is the contribution of career at time \(t\)
\(\epsilon_t\) is the contribution of the job at time \(t\)
At the start of time \(t\), a worker has the following options
retain a current (career, job) pair \((\theta_t, \epsilon_t)\) — referred to hereafter as “stay put”
retain a current career \(\theta_t\) but redraw a job \(\epsilon_t\) — referred to hereafter as “new job”
redraw both a career \(\theta_t\) and a job \(\epsilon_t\) — referred to hereafter as “new life”
Draws of \(\theta\) and \(\epsilon\) are independent of each other and past values, with
\(\theta_t \sim F\)
\(\epsilon_t \sim G\)
Notice that the worker does not have the option to retain a job but redraw a career — starting a new career always requires starting a new job.
A young worker aims to maximize the expected sum of discounted wages
subject to the choice restrictions specified above.
Let \(v(\theta, \epsilon)\) denote the value function, which is the maximum of (46.1) overall feasible (career, job) policies, given the initial state \((\theta, \epsilon)\).
The value function obeys
where
Evidently \(I\), \(II\) and \(III\) correspond to “stay put”, “new job” and “new life”, respectively.
46.2.1. Parameterization#
As in [Ljungqvist and Sargent, 2018], section 6.5, we will focus on a discrete version of the model, parameterized as follows:
both \(\theta\) and \(\epsilon\) take values in the set
jnp.linspace(0, B, grid_size)— an even grid of points between \(0\) and \(B\) inclusivegrid_size = 50B = 5β = 0.95
The distributions \(F\) and \(G\) are discrete distributions
generating draws from the grid points jnp.linspace(0, B, grid_size).
A very useful family of discrete distributions is the Beta-binomial family, with probability mass function
Interpretation:
draw \(q\) from a Beta distribution with shape parameters \((a, b)\)
run \(n\) independent binary trials, each with success probability \(q\)
\(p(k \,|\, n, a, b)\) is the probability of \(k\) successes in these \(n\) trials
Nice properties:
very flexible class of distributions, including uniform, symmetric unimodal, etc.
only three parameters
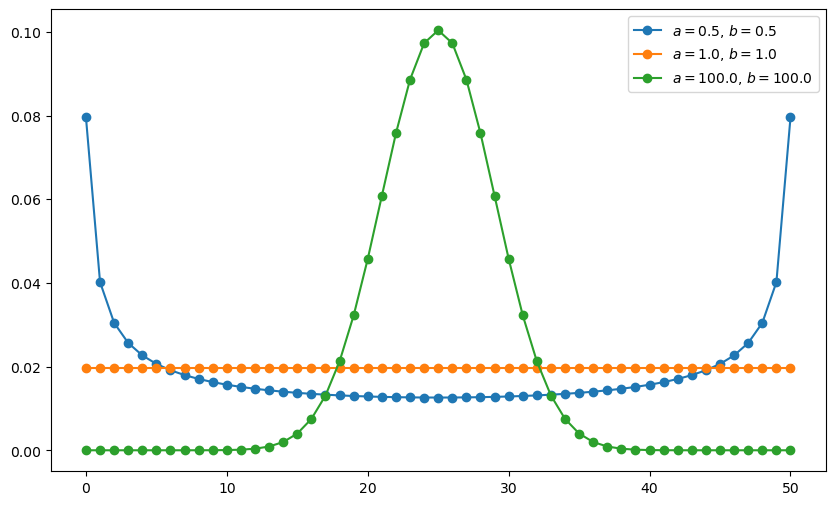
Here’s a figure showing the effect on the pmf of different shape parameters when \(n=50\).
def gen_probs(n, a, b):
probs = jnp.zeros(n+1)
k_vals = jnp.arange(n+1)
probs = jnp.array([binom(n, k) * beta(k + a, n - k + b) / beta(a, b) for k in range(n+1)])
return probs
n = 50
a_vals = [0.5, 1, 100]
b_vals = [0.5, 1, 100]
fig, ax = plt.subplots(figsize=(10, 6))
for a, b in zip(a_vals, b_vals):
ab_label = f'$a = {a:.1f}$, $b = {b:.1f}$'
ax.plot(list(range(0, n+1)), gen_probs(n, a, b), '-o', label=ab_label)
ax.legend()
plt.show()
46.3. Implementation#
We will first create a JAX-compatible model structure using NamedTuple to store
the model parameters and computed distributions.
class CareerWorkerProblem(NamedTuple):
β: float # Discount factor
B: float # Upper bound
grid_size: int # Grid size
θ: jnp.ndarray # Set of θ values
ε: jnp.ndarray # Set of ε values
F_probs: jnp.ndarray # Probabilities for F distribution
G_probs: jnp.ndarray # Probabilities for G distribution
F_mean: float # Mean of F distribution
G_mean: float # Mean of G distribution
def create_career_worker_problem(B=5.0, β=0.95, grid_size=50,
F_a=1, F_b=1, G_a=1, G_b=1):
"""
Factory function to create a CareerWorkerProblem instance.
"""
θ = jnp.linspace(0, B, grid_size) # Set of θ values
ε = jnp.linspace(0, B, grid_size) # Set of ε values
F_probs = jnp.array(BetaBinomial(grid_size - 1, F_a, F_b).pdf())
G_probs = jnp.array(BetaBinomial(grid_size - 1, G_a, G_b).pdf())
F_mean = θ @ F_probs
G_mean = ε @ G_probs
return CareerWorkerProblem(
β=β, B=B, grid_size=grid_size,
θ=θ, ε=ε,
F_probs=F_probs, G_probs=G_probs,
F_mean=F_mean, G_mean=G_mean
)
The following functions implement the Bellman operator \(T\) and the greedy policy function using JAX.
In this model, \(T\) is defined by \(Tv(\theta, \epsilon) = \max\{I, II, III\}\), where \(I\), \(II\) and \(III\) are as given in (46.2).
@jax.jit
def Q(θ_grid, ε_grid, β, v, F_probs, G_probs, F_mean, G_mean):
# Option 1: Stay put
v1 = θ_grid + ε_grid + β * v
# Option 2: New job (keep θ, new ε)
ev_new_job = jnp.dot(v, G_probs) # Expected value for each θ
v2 = θ_grid + G_mean + β * ev_new_job[:, jnp.newaxis]
# Option 3: New life (new θ and new ε)
ev_new_life = jnp.dot(F_probs, jnp.dot(v, G_probs))
v3 = jnp.full_like(v, G_mean + F_mean + β * ev_new_life)
return v1, v2, v3
@jax.jit
def bellman_operator(model, v):
"""
The Bellman operator for the career choice model.
"""
θ, ε, β = model.θ, model.ε, model.β
F_probs, G_probs = model.F_probs, model.G_probs
F_mean, G_mean = model.F_mean, model.G_mean
v1, v2, v3 = Q(
*jnp.meshgrid(θ, ε, indexing='ij'),
β, v, F_probs, G_probs, F_mean, G_mean
)
return jnp.maximum(jnp.maximum(v1, v2), v3)
@jax.jit
def get_greedy_policy(model, v):
"""
Computes the greedy policy given the value function.
* Policy function where 1=stay put, 2=new job, 3=new life
"""
θ, ε, β = model.θ, model.ε, model.β
F_probs, G_probs = model.F_probs, model.G_probs
F_mean, G_mean = model.F_mean, model.G_mean
v1, v2, v3 = Q(
*jnp.meshgrid(θ, ε, indexing='ij'),
β, v, F_probs, G_probs, F_mean, G_mean
)
# Stack the value arrays and find argmax along first axis
values = jnp.stack([v1, v2, v3], axis=0)
# +1 because actions are 1, 2, 3 not 0, 1, 2
policy = jnp.argmax(values, axis=0) + 1
return policy
Lastly, solve_model will take an instance of CareerWorkerProblem and
iterate using the Bellman operator to find the fixed point of the Bellman equation.
def solve_model(model, tol=1e-4, max_iter=1000):
"""
Solve the career choice model using JAX.
"""
# Initial guess
v = jnp.full((model.grid_size, model.grid_size), 100.0)
error = tol + 1
i = 0
while i < max_iter and error > tol:
v_new = bellman_operator(model, v)
error = jnp.max(jnp.abs(v_new - v))
v = v_new
i += 1
return v
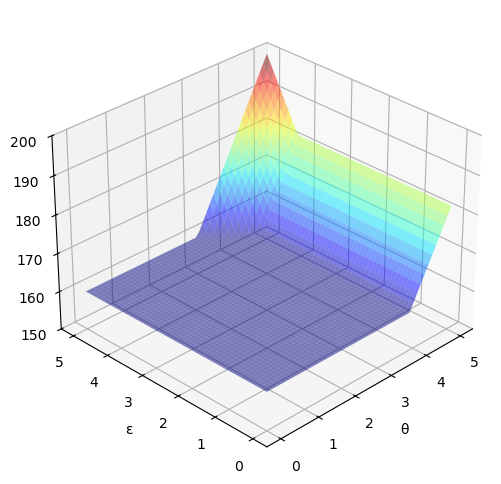
Here’s the solution to the model – an approximate value function
model = create_career_worker_problem()
v_star = solve_model(model)
greedy_star = get_greedy_policy(model, v_star)
fig = plt.figure(figsize=(8, 6))
ax = fig.add_subplot(111, projection='3d')
tg, eg = jnp.meshgrid(model.θ, model.ε)
ax.plot_surface(tg,
eg,
v_star.T,
cmap=cm.jet,
alpha=0.5,
linewidth=0.25)
ax.set(xlabel='θ', ylabel='ε', zlim=(150, 200))
ax.view_init(ax.elev, 225)
plt.show()
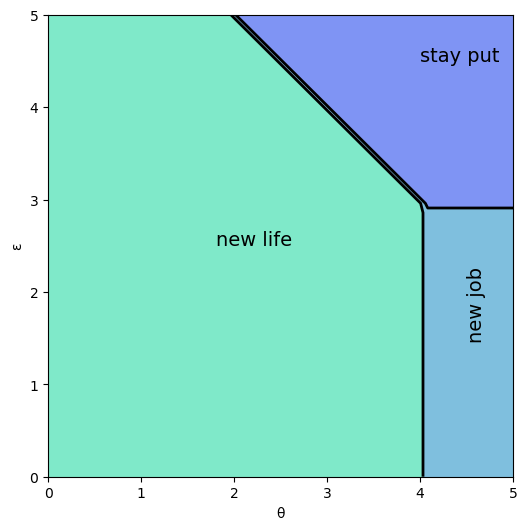
And here is the optimal policy
fig, ax = plt.subplots(figsize=(6, 6))
tg, eg = jnp.meshgrid(model.θ, model.ε)
lvls = (0.5, 1.5, 2.5, 3.5)
ax.contourf(tg, eg, greedy_star.T, levels=lvls, cmap=cm.winter, alpha=0.5)
ax.contour(tg, eg, greedy_star.T, colors='k', levels=lvls, linewidths=2)
ax.set(xlabel='θ', ylabel='ε')
ax.text(1.8, 2.5, 'new life', fontsize=14)
ax.text(4.5, 2.5, 'new job', fontsize=14, rotation='vertical')
ax.text(4.0, 4.5, 'stay put', fontsize=14)
plt.show()
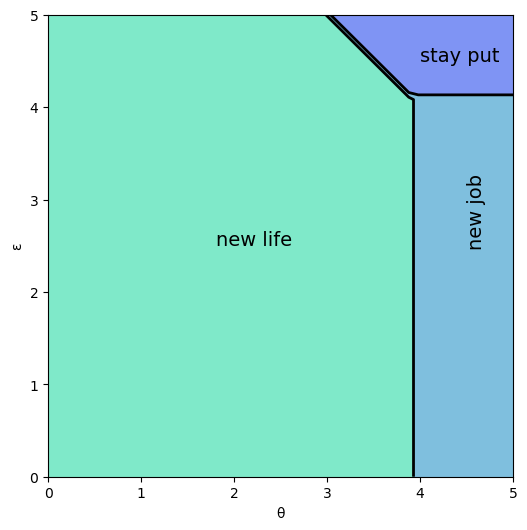
Interpretation:
If both job and career are poor or mediocre, the worker will experiment with a new job and new career.
If career is sufficiently good, the worker will hold it and experiment with new jobs until a sufficiently good one is found.
If both job and career are good, the worker will stay put.
Notice that the worker will always hold on to a sufficiently good career, but not necessarily hold on to even the best paying job.
The reason is that high lifetime wages require both variables to be large, and the worker cannot change careers without changing jobs.
Sometimes a good job must be sacrificed in order to change to a better career.
46.4. Exercises#
Exercise 46.1
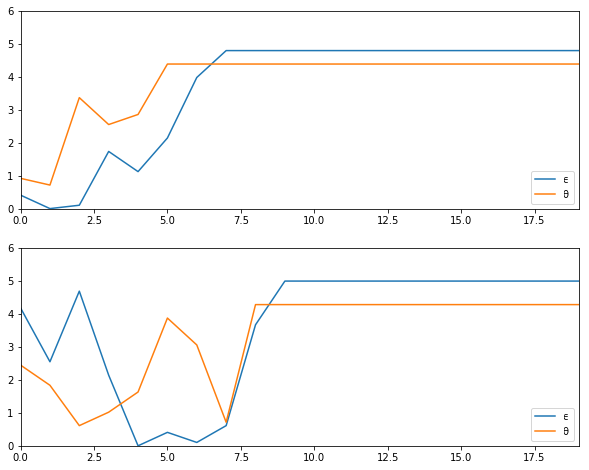
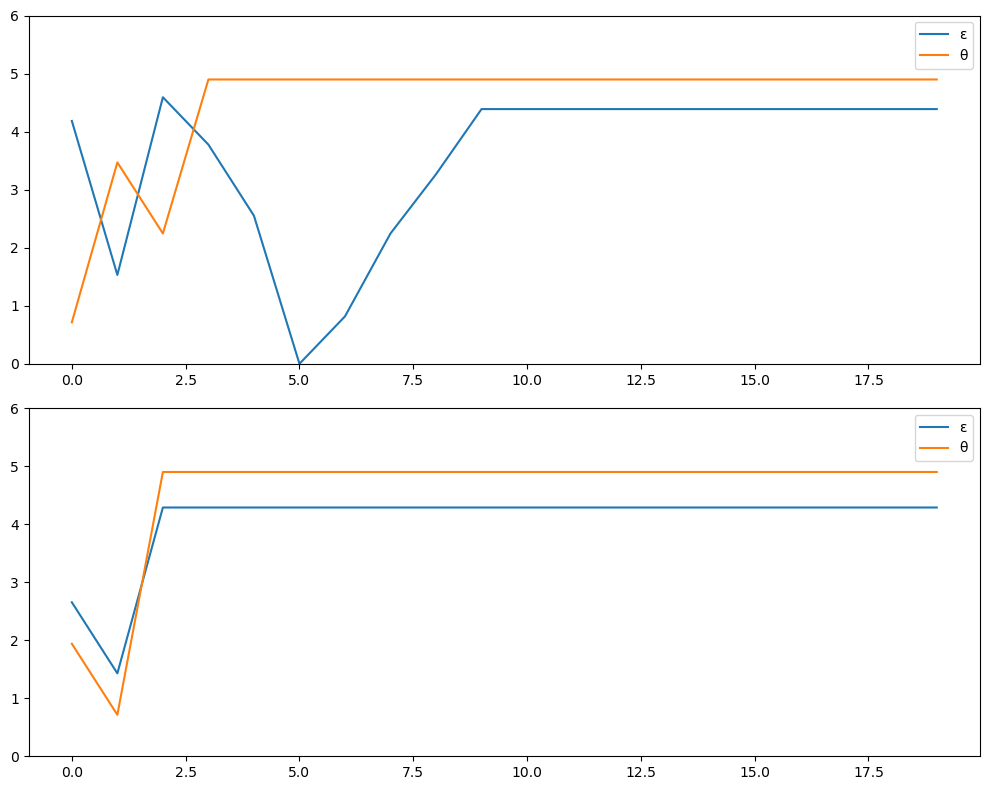
Using the default parameterization in the class CareerWorkerProblem,
generate and plot typical sample paths for \(\theta\) and \(\epsilon\)
when the worker follows the optimal policy.
In particular, modulo randomness, reproduce the following figure (where the horizontal axis represents time)
Hint
To generate the draws from the distributions \(F\) and \(G\), use quantecon.jr.draw().
Solution to Exercise 46.1
Simulate job/career paths.
In reading the code, recall that optimal_policy[i, j] = policy at
\((\theta_i, \epsilon_j)\) = either 1, 2 or 3; meaning ‘stay put’,
‘new job’ and ‘new life’.
model = create_career_worker_problem()
F = jnp.cumsum(jnp.asarray(model.F_probs))
G = jnp.cumsum(jnp.asarray(model.G_probs))
v_star = solve_model(model)
greedy_star = jnp.asarray(get_greedy_policy(model, v_star))
def draw_from_cdf(key, cdf):
u = jr.uniform(key)
return jnp.searchsorted(cdf, u, side="left")
def gen_path(optimal_policy, F, G, model, t=20, key=None):
if key is None:
key = jr.PRNGKey(0)
i = 0
j = 0
theta_idx = []
eps_idx = []
for _ in range(t):
a = optimal_policy[i, j]
key, k1, k2 = jr.split(key, 3)
if a == 1: # Stay put
pass
elif a == 2: # New job
j = draw_from_cdf(k1, G)
else: # New life
i = draw_from_cdf(k1, F)
j = draw_from_cdf(k2, G)
theta_idx.append(i)
eps_idx.append(j)
theta_idx = jnp.array(theta_idx, dtype=jnp.int32)
eps_idx = jnp.array(eps_idx, dtype=jnp.int32)
return model.θ[theta_idx], model.ε[eps_idx], key
key = jr.PRNGKey(42)
fig, axes = plt.subplots(2, 1, figsize=(10, 8))
for ax in axes:
key, subkey = jr.split(key)
θ_path, ε_path, _ = gen_path(greedy_star, F, G, model, key=subkey)
ax.plot(ε_path, label='ε')
ax.plot(θ_path, label='θ')
ax.set_ylim(0, 6)
ax.legend(loc='upper right')
plt.tight_layout()
plt.show()
Exercise 46.2
Let’s now consider how long it takes for the worker to settle down to a permanent job, given a starting point of \((\theta, \epsilon) = (0, 0)\).
In other words, we want to study the distribution of the random variable
Evidently, the worker’s job becomes permanent if and only if \((\theta_t, \epsilon_t)\) enters the “stay put” region of \((\theta, \epsilon)\) space.
Letting \(S\) denote this region, \(T^*\) can be expressed as the first passage time to \(S\) under the optimal policy:
Collect 25,000 draws of this random variable and compute the median (which should be about 7).
Repeat the exercise with \(\beta=0.99\) and interpret the change.
Solution to Exercise 46.2
The median for the original parameterization can be computed as follows
model = create_career_worker_problem()
F = jnp.cumsum(jnp.asarray(model.F_probs))
G = jnp.cumsum(jnp.asarray(model.G_probs))
v_star = solve_model(model)
greedy_star = jnp.asarray(get_greedy_policy(model, v_star))
def passage_time(optimal_policy, F, G, key):
def cond(state):
i, j, t, key = state
return optimal_policy[i, j] != 1
def body(state):
i, j, t, key = state
a = optimal_policy[i, j]
key, k1, k2 = jr.split(key, 3)
new_j = draw_from_cdf(k1, G)
new_i = draw_from_cdf(k2, F)
i = jnp.where(a == 3, new_i, i)
j = jnp.where((a == 2) | (a == 3), new_j, j)
return i, j, t + 1, key
i, j, t, _ = jax.lax.while_loop(cond, body, (0, 0, 0, key))
return t
def median_time(optimal_policy, F, G, M=25000, seed=0):
keys = jr.split(jr.PRNGKey(seed), M)
times = jax.vmap(lambda k: passage_time(optimal_policy, F, G, k))(keys)
return jnp.median(times)
median_time(greedy_star, F, G)
Array(7., dtype=float32)
To compute the median with \(\beta=0.99\) instead of the default
value \(\beta=0.95\), replace model = create_career_worker_problem() with
model = create_career_worker_problem(β=0.99).
The medians are subject to randomness but should be about 7 and 14 respectively.
Not surprisingly, more patient workers will wait longer to settle down to their final job.
Exercise 46.3
Set the parameterization to G_a = G_b = 100 and generate a new optimal policy
figure – interpret.
Solution to Exercise 46.3
Here is one solution
model = create_career_worker_problem(G_a=100, G_b=100)
v_star = solve_model(model)
greedy_star = get_greedy_policy(model, v_star)
fig, ax = plt.subplots(figsize=(6, 6))
tg, eg = jnp.meshgrid(model.θ, model.ε)
lvls = (0.5, 1.5, 2.5, 3.5)
ax.contourf(tg, eg, greedy_star.T, levels=lvls, cmap=cm.winter, alpha=0.5)
ax.contour(tg, eg, greedy_star.T, colors='k', levels=lvls, linewidths=2)
ax.set(xlabel='θ', ylabel='ε')
ax.text(1.8, 2.5, 'new life', fontsize=14)
ax.text(4.5, 1.5, 'new job', fontsize=14, rotation='vertical')
ax.text(4.0, 4.5, 'stay put', fontsize=14)
plt.show()
In the new figure, you see that the region for which the worker stays put has grown because the distribution for \(\epsilon\) has become more concentrated around the mean, making high-paying jobs less realistic.